[백준] 최소비용 구하기 2 (11779)(kotlin)

문제 설명

백준 11779번 문제 링크

입력 및 출력

» 입력

• 첫째 줄에 도시의 개수 n(1≤n≤1,000)이 주어지고 둘째 줄에는 버스의 개수 m(1≤m≤100,000)이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가 주어진다. 그리고 그 다음에는 도착지의 도시 번호가 주어지고 또 그 버스 비용이 주어진다. 버스 비용은 0보다 크거나 같고, 100,000보다 작은 정수이다. 그리고 m+3째 줄에는 우리가 구하고자 하는 구간 출발점의 도시번호와 도착점의 도시번호가 주어진다.

» 출력

• 첫째 줄에 출발 도시에서 도착 도시까지 가는데 드는 최소 비용을 출력한다. 둘째 줄에는 그러한 최소 비용을 갖는 경로에 포함되어있는 도시의 개수를 출력한다. 출발 도시와 도착 도시도 포함한다. 셋째 줄에는 최소 비용을 갖는 경로를 방문하는 도시 순서대로 출력한다.

예제 입출력(테스트케이스)

입력	출력
5 8 1 2 2 1 3 3 1 4 1 1 5 10 2 4 2 3 4 1 3 5 1 4 5 3 1 5	4 3 1 3 5

문제 풀이1 (Dijkstra - Adjacency List)

풀이 참고

import java.util.PriorityQueue

class Node(val destination: Int, val cost: Int): Comparable<Node> {
    override fun compareTo(other: Node): Int {
        return this.cost - other.cost
    }
}


fun main(args: Array<String>) = with(System.`in`.bufferedReader()) {
    val n = readLine().toInt()
    val adjList = Array(n + 1) { PriorityQueue<Node>() }

    repeat(readLine().toInt()) {
        val (s, d, c) = readLine().split(" ").map { it.toInt() }
        adjList[s].add(Node(d, c))
    }

    val (start, destination) = readLine().split(" ").map { it.toInt() }
    val min = dijkstra(start, destination, n, adjList)
    val paths = searchPath(start, destination, min[1])

    println(min[0][destination])
    println(paths.size)
    println(paths.joinToString(" "))
}

fun dijkstra(start: Int, end: Int, n: Int ,adjList: Array<PriorityQueue<Node>>): Array<IntArray> {
    val q = PriorityQueue<Node>()
    val check = BooleanArray(n + 1)
    val distance = IntArray(n + 1) { Int.MAX_VALUE }
    val parent = IntArray(n + 1)

    q.add(Node(start, 0))
    distance[start] = 0

    while (q.isNotEmpty()) {
        val now = q.poll()

        if (check[now.destination]) continue
        check[now.destination] = true

        for (node in adjList[now.destination]) {
            if (distance[node.destination] >= distance[now.destination] + node.cost) {
                distance[node.destination] = distance[now.destination] + node.cost
                q.add(Node(node.destination, distance[node.destination]))

                parent[node.destination] = now.destination
            }
        }
    }

    return arrayOf(distance, parent)
}

fun searchPath(start: Int, end: Int, parent: IntArray): IntArray {
    val list = mutableListOf<Int>()
    var destination = end

    while (start != destination) {
        list.add(destination)
        destination = parent[destination]
    }

    list.add(start)

    return list.reversed().toIntArray()
}

문제 풀이1 시뮬레이션

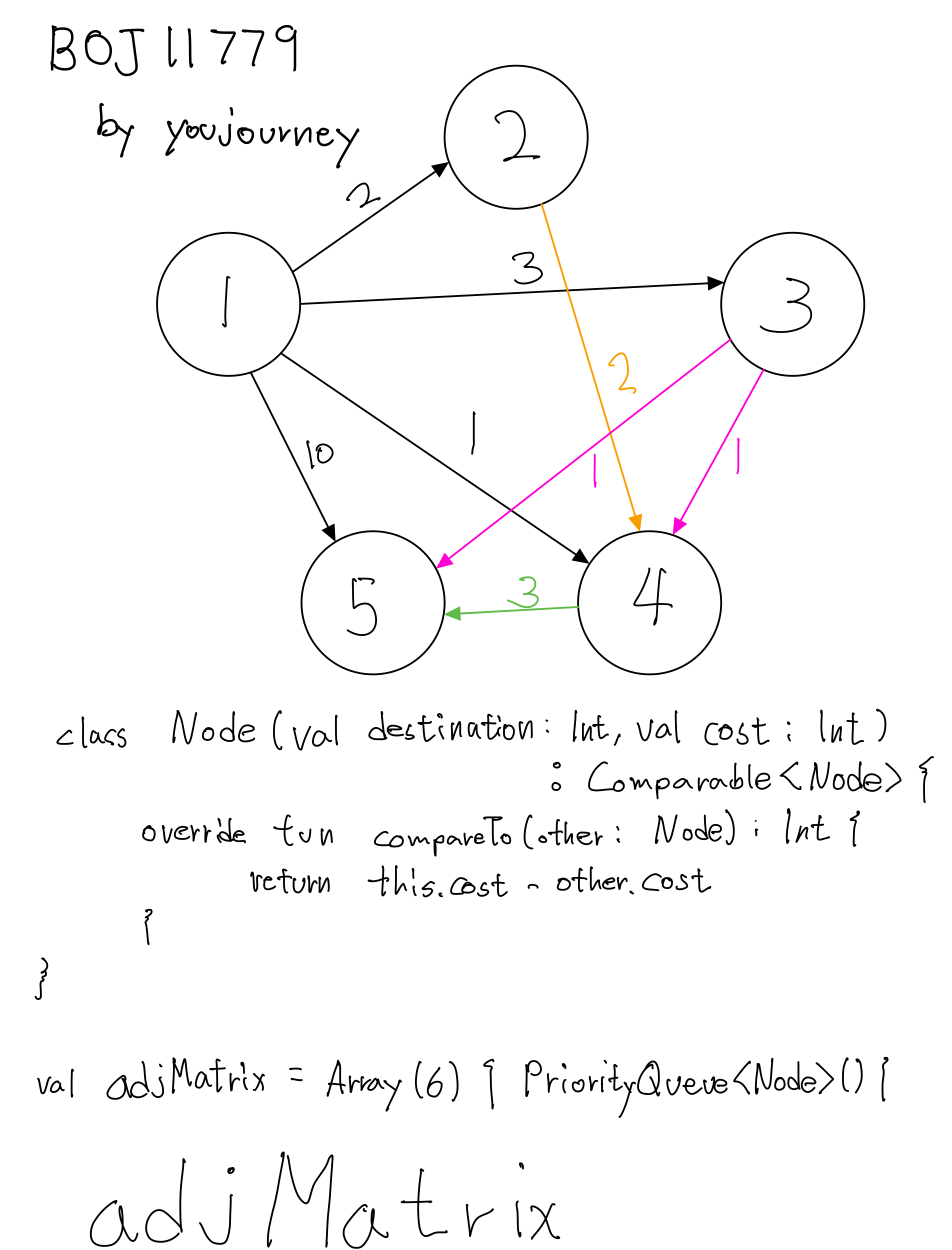
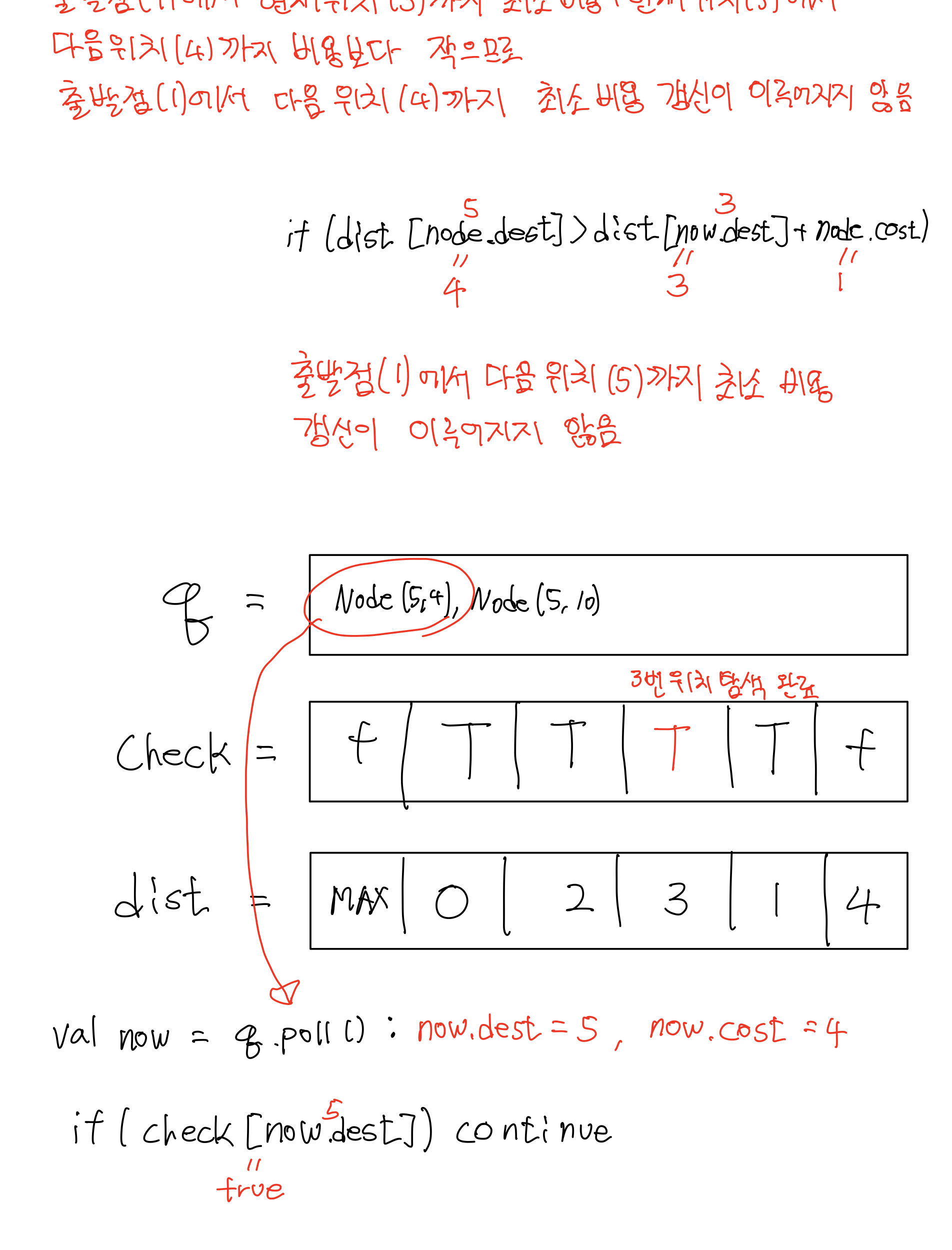
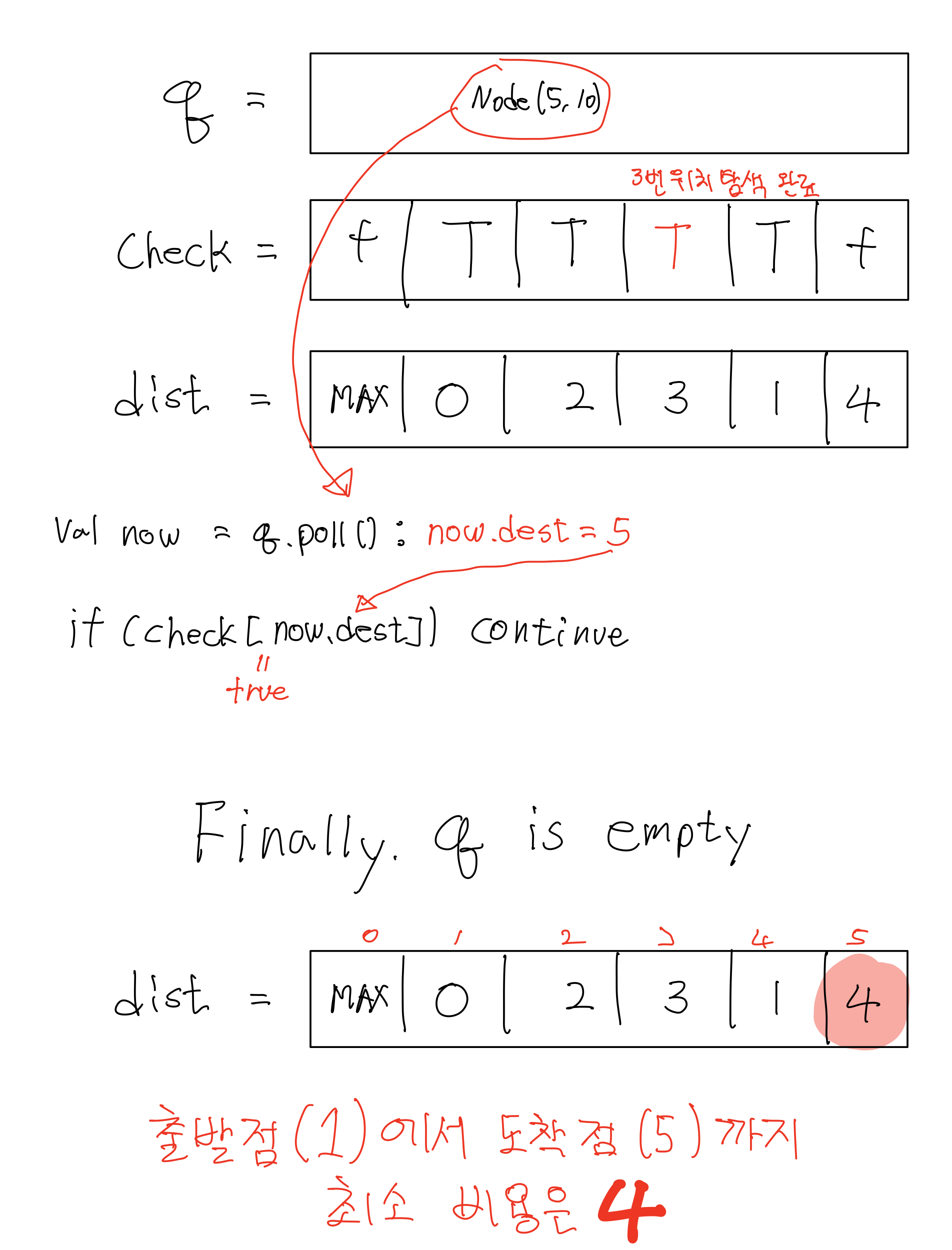
문제 풀이2 (미완성 코드)(Dijkstra - Adjacency Matrix)

fun main(args: Array<String>) = with(System.`in`.bufferedReader()) {
    val n = readLine().toInt()
    val adjMatrix = Array(n + 1) { IntArray(n + 1) { Int.MAX_VALUE } }

    repeat(readLine().toInt()) {
        val (s, d, c) = readLine().split(" ").map { it.toInt() }
        adjMatrix[s][d] = c
    }

    val (start, destination) = readLine().split(" ").map { it.toInt() }

    var route = Array(n + 1) { intArrayOf() }
    for (i in 1..n) {
        route[i] = dijkstra(n, start, adjMatrix[i], adjMatrix)
    }

    println(route[start][destination])
}

fun dijkstra(n: Int, start: Int, distance: IntArray, adjMatrix: Array<IntArray>): IntArray {
    val check = BooleanArray(n + 1)
    check[start] = true
    distance[start] = 0

    repeat(n - 1) {
        var min = Int.MAX_VALUE
        var min_index = 0

        for (i in 1..n) {
            if (check[i]) continue
            if (min > distance[i]) {
                min = distance[i]
                min_index = i
            }
        }

        check[min_index] = true

        for (next in 1..n) {
            if (adjMatrix[min_index][next] == Int.MAX_VALUE) continue
            if (adjMatrix[min_index][next] == 0) continue
            if (distance[next] > distance[min_index] + adjMatrix[min_index][next]) {
                distance[next] = distance[min_index] + adjMatrix[min_index][next]
            }
        }
    }

    return distance
}