[백준] 베시와 데이지 (16431)(kotlin)

원본 문제

문제 설명

농부 존은 소 베시와 소 데이지를 키우고 있습니다.

두 소는 자유롭게 1,000 × 1,000 2차원 격자 목초지를 누비며 놀고 있습니다. 농부 존이 종을 치면 베시와 데이지가 농부 존이 있는 곳으로 달려갑니다.

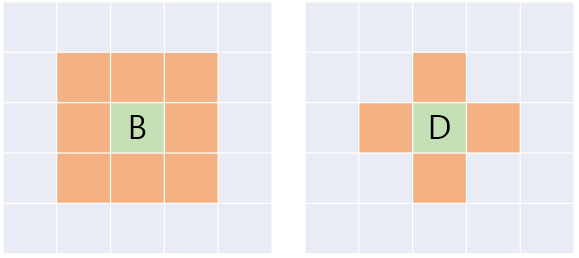
베시가 B에 있을 때 1초 후에 움직일 수 있는 칸과 데이지가 D에 있을 때 1초 후에 움직일 수 있는 칸을 나타낸 그림

베시는 1초 후에 꼭짓점을 공유하는 8개의 칸 중 하나로 이동할 수 있고 데이지는 1초 후에 변을 공유하는 4개의 칸 중 하나로 이동할 수 있습니다. 칸들은 충분히 넓어서 칸 하나에도 베시와 데이지 그리고 존이 같이 서 있을 수 있습니다.

베시와 데이지 두 소 모두 최단 경로로 존에게 갈 때 어떤 소가 더 빨리 도착할까요?

입력

첫 번째 줄에 베시의 좌표 Br, Bc (1 ≤ Br, Bc ≤ 1,000) 이 주어집니다.

두 번째 줄에 데이지의 좌표 Dr, Dc (1 ≤ Dr, Dc ≤ 1,000) 이 주어집니다.

세 번째 줄에 존의 좌표 Jr, Jc (1 ≤ Jr, Jc ≤ 1,000) 이 주어집니다.

처음에 존이 있는 칸에는 베시와 데이지가 없음이 보장됩니다.

출력

첫 번째 줄에 베시가 더 빨리 도착하면 ‘bessie’, 데이지가 더 빨리 도착하면 ‘daisy’, 동시에 도착하면 ‘tie’ 를 출력합니다.

테스트 케이스

입력	출력
3 5 1 1 2 3	bessie
13 13 11 11 11 12	daisy
4 5 5 4 4 4	tie

문제 풀이1

import java.util.Scanner
import kotlin.math.absoluteValue
import kotlin.math.min

fun main(args: Array<String>) {
    val sc = Scanner(System.`in`)
    val bx = sc.nextInt()
    val by = sc.nextInt()
    val dx = sc.nextInt()
    val dy = sc.nextInt()
    val jx = sc.nextInt()
    val jy = sc.nextInt()


    val bessieTime = if (jx - bx == jy - by) (jx - bx).absoluteValue
    else {
        val x = (jx - bx).absoluteValue
        val y = (jy - by).absoluteValue
        (x - y).absoluteValue + min(x, y)
    }
    val daisyTime = (jx - dx).absoluteValue + (jy - dy).absoluteValue

    when {
        daisyTime < bessieTime -> println("daisy")
        daisyTime > bessieTime -> println("bessie")
        else -> println("tie")
    }
}

문제 풀이2

import java.util.Scanner
import kotlin.math.max
import kotlin.math.abs

fun main(args: Array<String>) {
    val sc = Scanner(System.`in`)
    val bx = sc.nextInt()
    val by = sc.nextInt()
    val dx = sc.nextInt()
    val dy = sc.nextInt()
    val jx = sc.nextInt()
    val jy = sc.nextInt()


    val bessieTime = max(abs(bx - jx), abs(by - jy))
    val daisyTime = abs(dx - jx) + abs(dy - jy)

    when {
        daisyTime < bessieTime -> println("daisy")
        daisyTime > bessieTime -> println("bessie")
        else -> println("tie")
    }
}