[프로그래머스] 2021 카카오 채용연계형 인턴십 > 미로 탈출 (81304)
문제 설명
신규 게임 ‘카카오 미로 탈출’이 출시되어, 라이언이 베타테스터로 참가했습니다.
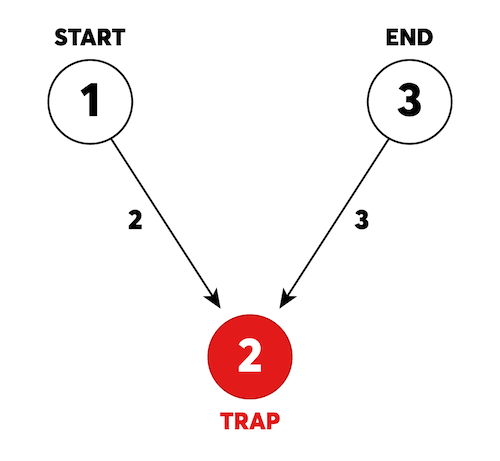
위 예시 그림은 카카오 미로 탈출의 초기 상태를 나타냅니다. 1번부터 3번까지 번호가 붙어있는 3개의 방이 있고, 방과 방 사이를 연결하는 길에는 이동하는데 걸리는 시간이 표시되어 있습니다. 길은 화살표가 가리키는 방향으로만 이동할 수 있습니다. 미로에는 함정이 존재하며, 함정으로 이동하면, 이동한 함정과 연결된 모든 화살표의 방향이 바뀝니다.
출발지점인 1번 방에서 탈출이 가능한 3번 방까지 이동해야 합니다. 탈출하는데 걸리는 최소 시간을 구하려고 합니다.
-
그림의 원은 방을 나타내며 원 안의 숫자는 방 번호를 나타냅니다.
- 방이
n개일 때, 방 번호는 1부터n까지 사용됩니다.
- 방이
-
화살표에 표시된 숫자는 방과 방 사이를 이동할 때 걸리는 시간을 나타냅니다.
- 화살표가 가리키고 있는 방향으로만 이동이 가능합니다. 즉, 위 그림에서 2번 방에서 1번 방으로는 이동할 수 없습니다.
-
그림에 표시된 빨간색 방인
2번 방은 함정입니다.
- 함정 방으로 이동하는 순간, 이동한 함정 방과 연결되어있는 모든 길의 방향이 반대가 됩니다.
- 위 그림
1번 방에서2번 방으로 이동하는 순간1에서2로 이동할 수 있던 길은2에서1로 이동할 수 있는 길로 바뀌고,3에서2로 이동할 수 있던 길은2에서3으로 이동할 수 있는 길로 바뀝니다. - 똑같은 함정 방을 두 번째 방문하게 되면 원래 방향의 길로 돌아옵니다. 즉, 여러 번 방문하여 계속 길의 방향을 반대로 뒤집을 수 있습니다.
-
미로를 탈출하는데 필요한 최단 시간은 다음과 같습니다.
- 1→2: 2번 방으로 이동합니다. 이동 시간은 2입니다.
- 함정 발동: 2번 방과 연결된 모든 길의 방향이 반대가 됩니다.
- 2→3: 3번 방으로 이동합니다. 이동 시간은 3입니다.
- 탈출에 성공했습니다. 총 이동시간은 5입니다.
방의 개수를 나타내는 정수 n, 출발 방의 번호 start, 도착 방의 번호 end, 통로와 이동시간을 나타내는 2차원 정수 배열 roads, 함정 방의 번호를 담은 정수 배열 traps이 매개변수로 주어질 때, 미로를 탈출하는데 필요한 최단 시간을 return 하도록 solution 함수를 완성해주세요.
제한사항
-
2 ≤
n≤ 1,000 -
1 ≤
start≤n -
1 ≤
end≤n -
1 ≤
roads의 행 길이 ≤ 3,000 -
roads의 행은 [P, Q, S]로 이루어져 있습니다.
P에서Q로 갈 수 있는 길이 있으며, 길을 따라 이동하는데S만큼 시간이 걸립니다.- 1 ≤
P≤n - 1 ≤
Q≤n P≠Q- 1 ≤
S≤ 3,000 - 서로 다른 두 방 사이에 직접 연결된 길이 여러 개 존재할 수도 있습니다.
-
0 ≤
traps의 길이 ≤ 10
- 1 ≤
traps의 원소 ≤n - 시작 방과 도착 방은 함정이 아닙니다.
- 1 ≤
- 항상 미로를 탈출할 수 있는 경우만 주어집니다.
[입출력 예]
| n | start | end | roads | traps | result |
|---|---|---|---|---|---|
| 3 | 1 | 3 | [[1, 2, 2], [3, 2, 3]] | [2] | 5 |
| 4 | 1 | 4 | [[1, 2, 1], [3, 2, 1], [2, 4, 1]] | [2, 3] | 4 |
입출력 예1
문제 예시와 같습니다.
입출력 예2
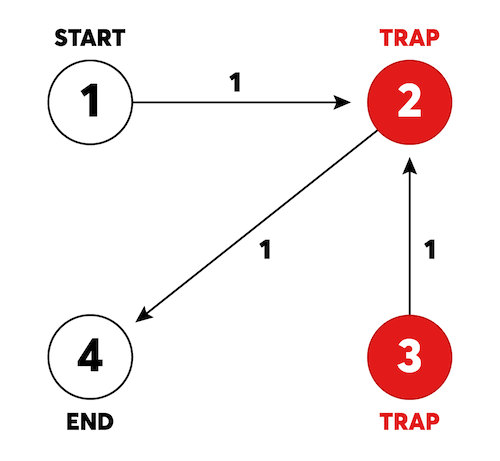
1 → 2 → 3 → 2 → 4 순서로 이동하면 됩니다. 총 이동시간은 4입니다.
문제 풀이 (KOTLIN)
정확성 : 69.2 / 100
import kotlin.math.min
class Solution {
var check: BooleanArray = booleanArrayOf()
fun solution(n: Int, start: Int, end: Int, roads: Array<IntArray>, traps: IntArray): Int {
val matrix = Array(n + 1) { IntArray(n + 1) { Int.MAX_VALUE } }
val distance = IntArray(n + 1) { Int.MAX_VALUE }
check = BooleanArray(n + 1) { false }
var go = start
var prev = 0
roads.forEach {
val (s, d, c) = it
matrix[s][d] = min(matrix[s][d], c)
}
distance[go] = 0
repeat(n) {
var min = Int.MAX_VALUE
for (i in 1..n) {
if (check[i]) continue
if (min > distance[i]) {
min = distance[i]
go = i
}
}
check[go] = true
for (next in 1..n) {
if (matrix[go][next] == Int.MAX_VALUE) {
continue
}
if (distance[next] > distance[go] + matrix[go][next]) {
distance[next] = distance[go] + matrix[go][next]
if (traps.contains(next)) {
if (traps.contains(go)) {
check[prev] = false
}
activatesTrap(next, matrix, n)
}
}
}
prev = go
}
return distance[end]
}
fun activatesTrap(trap: Int, matrix: Array<IntArray>, n: Int) {
for (i in 1..n) {
if (matrix[i][trap] != matrix[trap][i]) {
val temp = matrix[i][trap]
matrix[i][trap] = matrix[trap][i]
matrix[trap][i] = temp
}
}
}
}
문제 풀이 (SWIFT)
정확성 : 69.2 / 100
!comparer(nodes[right], nodes[index]) {
nodes.swapAt(right, index)
index = right
} else if !comparer(nodes[left], nodes[index]){
nodes.swapAt(left, index)
index = left
} else {
break
}
} else if left < nodes.count {
if !comparer(nodes[left], nodes[index]) {
nodes.swapAt(left, index)
index = left
} else {
break
}
} else {
break
}
}
return result
}
}
extension PriorityQueue where T: Comparable {
init() {
self.init(comparer: >)
}
}
struct Node: Comparable {
static func < (lhs: Node, rhs: Node) -> Bool {
lhs.cost < rhs.cost
}
let node: Int // 현재 방문 노드 index
let cost: Int // 시작점부터 현재노드까지 걸린 총 비용
let trapState: Int
}
func dijkstra(_ n: Int, _ graph: [[Int]], _ src: Int, _ dst: Int, _ traps: [I
var pq = PriorityQueue<Node>()
var visited = [[Bool]](repeating: [Bool](repeating: false, count: n + 1),
pq.enqueue(Node(node: src, cost: 0, trapState: 0))
while !pq.isEmpty {
let current = pq.dequeue()
let u = current!.node
let w = current!.cost
var state = current!.trapState
if u == dst { return w }
if visited[u][state] { continue }
visited[u][state] = true
var currTrapped = false
var trapped = [Int : Bool]()
for i in 0..<traps.count {
let bit = 1 << i
if state & bit > 0 {
if traps[i] == u {
state &= ~bit
} else {
trapped[traps[i]] = true
}
} else {
if traps[i] == u {
state |= bit
trapped[traps[i]] = true
currTrapped = true
}
}
}
for v in 1...n {
if v == u { continue }
let nextTrapped = trapped[v] ?? false
if currTrapped == nextTrapped {
if graph[u][v] != Int.max {
pq.enqueue(Node(node: v, cost: w + graph[u][v], trapState
}
} else {
if graph[v][u] != Int.max {
pq.enqueue(Node(node: v, cost: w + graph[v][u], trapState
}
}
}
}
return Int.max
}
func solution(_ n:Int, _ start:Int, _ end:Int, _ roads:[[Int]], _ traps:[Int]
var graph = [[Int]](repeating: [Int](repeating: Int.max, count: n + 1), c
for data in roads {
let u = data[0]
let v = data[1]
let w = data[2]
if w < graph[u][v] {
graph[u][v] = w
}
}
return dijkstra(n, graph, start, end, traps)
}
